
在更好(hǎo)地理(lǐ)解nσ(以下(xià)稱n Sigma)之前,我們應該知(zhī)道(dào)XRF分析是一種統計(jì)方法。與大(dà)多數統計(jì)數據一樣,樣本的數量越大(dà),統計(jì)的結果越準确。例如,我們扔一枚硬币。扔出硬币後,在硬币落下(xià)時(shí),我們預計(jì)出現(xiàn)正面和(hé)反面的概率都是50%。在我們隻扔了(le)4次的情況下(xià),如果我們得到(dào)的正面與反面的比率爲3:1(即得到(dào)正面的概率爲75%),就是得到(dào)正面的概率比預期多了(le)25%,我們并不會(huì)感到(dào)驚訝。如果我們扔了(le)一千次硬币,仍得到(dào)75%正面在上(shàng)的概率,那麽我們可以斷言這(zhè)枚硬币各部分的比重不一樣,如果不是這(zhè)樣的話(huà),我們預計(jì)得到(dào)的結果會(huì)更接近50/50的概率。
同樣的原則适用(yòng)于XRF分析。在X射線計(jì)數的開(kāi)始隻有少量的計(jì)數時(shí),統計(jì)數據的波動現(xiàn)象占主導地位。此時(shí)的頻譜參差不齊,很(hěn)難從(cóng)波動中區(qū)分出真正的波峰。随着時(shí)間的延長,計(jì)數在增加,而頻譜會(huì)變得更爲平滑。波峰明(míng)顯可見,統計(jì)的不确定性也(yě)在下(xià)降。我們可以得出結論:X射線越多,統計(jì)數據越準确。這(zhè)就解釋了(le)爲什(shén)麽X射線計(jì)數對(duì)于确保準确的XRF分析如此重要。
數學分析方法表明(míng):不确定性按平方反比減小(xiǎo)。例如,要将不确定性減少到(dào)三分之一(如:從(cóng)30 ppm降至10 ppm),我們需要将檢測時(shí)間延長9倍。進行短時(shí)檢測可以獲得較高(gāo)的檢測量,而進行長時(shí)檢測可以獲得更準确的結果,這(zhè)就需要由用(yòng)戶權衡兩種情況的相對(duì)優勢,做出适當的決定。
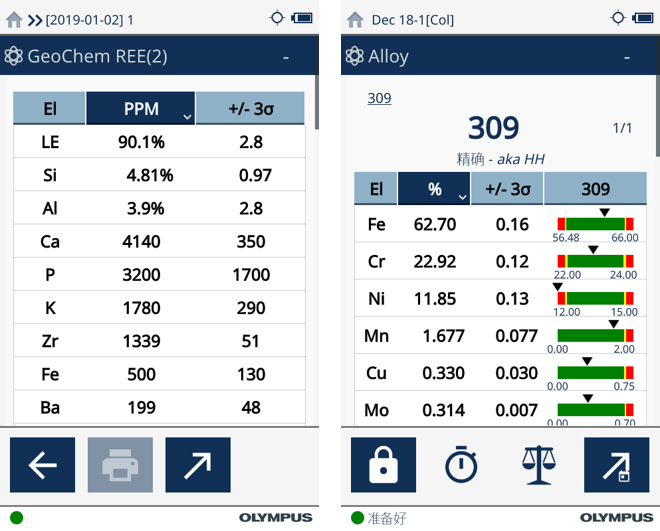
XRF分析儀計(jì)算(suàn)出不确定性,并在屏幕上(shàng)分析結果的旁邊顯示精密度(+/-讀數)——(在數學上(shàng)被稱爲σ,即Sigma),我們習慣稱之爲“誤差值”。Vanta可讓用(yòng)戶選擇“+/-”旁邊的Sigma值是1、2,還是3(默認值爲1)。随着檢測的進行,我們可以看(kàn)到(dào)+/-讀數值在不斷下(xià)降,最終,XRF分析儀會(huì)給出一個明(míng)确的結果。所以,n Sigma(+/-讀數)是分析結果非常重要的組成部分。
我們在評估分析結果時(shí),常常提到(dào)準确度和(hé)精密度。精密度是可重複性的一種度量,或者說一個檢測結果與另一個檢測結果的相近程度。準确度表明(míng)所獲得的結果是否準确地反映了(le)實際情況(接近真值)。手持式XRF分析儀在屏幕上(shàng)出現(xiàn)的 “+/-”列中彙報(bào)精密度。精密度主要是X射線計(jì)數的一個函數。爲了(le)增加計(jì)數,提高(gāo)精密度,我們可以延長檢測時(shí)間。我們也(yě)可以選用(yòng)一款提供更高(gāo)計(jì)數率的分析儀(例如:配備了(le)矽漂移X射線探測器的分析儀,而不是配備有PIN探測器的分析儀)。
n Sigma,也(yě)被用(yòng)來(lái)定義檢出限(LOD)和(hé)定量限(LOQ)。檢出限被定義爲測量不确定性的三倍。這(zhè)是确定存在所關注元素的99.6%置信度所對(duì)應的元素含量的阈限值。定量限被定義爲不确定性的十倍。定量限是可以對(duì)所顯示的值充滿信心的最低(dī)含量值,而不是僅能(néng)探測到(dào)的含量值。例如:我們檢測的是樣本中的Ni元素,1 sigma的+/-讀數值是5 ppm。3 Sigma的值應該是15ppm。如果我們要得到(dào)Ni元素确實存在的99.6%置信度,鎳元素的含量需要超過15ppm。如果我們要明(míng)确地測出鎳元素的含量,鎳元素的含量需要達到(dào)50 ppm。
現(xiàn)在,我們了(le)解了(le)Vanta分析儀上(shàng)關于nσ(n Sigma)的含義,所以在我們判讀XRF結果時(shí),需留意“+/-”列中的讀數,因爲這(zhè)些(xiē)讀數可以使我們清楚地知(zhī)道(dào)應該如何看(kàn)待所顯示的結果值。
